observations. Please see my last post Recipe for Disaster to see where this train of thought came from and I will be linking some conclusions together between this post and that one.
First, what the hell is a derivative?
Maybe you are familiar with this concept on calculus and maybe not. Here is the real background if you are interested (http://en.wikipedia.org/wiki/Derivative), but here is the 1 paragraph version that gives you an understanding for this post.
A function is a description of how a dependent variable (lets call it y) moves with respect to an independent variable (lets call it x). A straight line is a very simple example: y = slope*x + intercept. Or a parabola: y = x^2. A derivative tells you the instantaneous rate of change of that function as x changes. It is also the slope of the function, but rate of change is the key concept. A straight line is always changing at a constant value, hence its derivative is a constant number. The parabola has a negative slope for x < 0, has a slope of zero at x = 0, and has a positive slope for x > 0. The second derivative tells you the rate of change of the first derivative.
Okay, that was a bit abstract. So lets use a physical example. Position (or displacement) as a dependent variable tells you where you are with respect to time, the independent variable. The first derivative will tell you the rate of change of position with respect to time. This is the velocity, or speed. Everybody is familiar with this concept. The second derivative will tell you the rate of change of velocity with respect to time. This is the acceleration. Another familiar concept.
Now lets apply this concept to the stock market. I will specifically be using the S&P 500 here. The price is analogous to the position, and we will look at the first and second derivatives of price, to help us to understand the behavior of how the price is changing with time.
First, here is the chart:
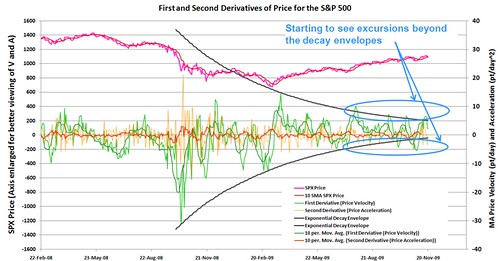
The price of the SPX is at the top of the chart in pink (I adjusted the left axis so the price would reside above the velocity and acceleration curves so that the chart would be more readable).
I did not calculate the velocity directly from the price action. It is too chaotic and would give just a big mess. So I calculated the 10 day Moving Average of the price (based on closing prices) and determined the velocity of that curve. For an additional bit of "smoothing" I am also plotting the 10 day MA of velocity just so the trend is a bit clearer, but I am working with the velocity as described above. The acceleration is calculated directly from the velocity, but I am also plotting a 10 day MA for the acceleration so you can see the trends (since it is also very spiky)
As a side note, the ROC (rate of change) indicator on Stockcharts gives you very similar "velocity" information. I am showing the data plotted myself since I am going through a more in depth study.
Important observations: The middle of last year was the market crash. This is by far the most important price action element on the 2 year chart. The move down was a violent freefall and you can see the associated velocity spike.
When I think about this move and try to assign it a physical corollary, I think of a football kick. A football is initially at rest and then the kicker kicks the ball to put it on its parabolic trajectory toward the goal posts. But what is of interest here is the dynamics and forces right at the time of the kick.
This system can be modeled as a first order Ordinary Differential Equation with a prescribed velocity as the initial condition. And for those who have done first order and second order ODE modeling of physical processes, the disturbance perturbs the system which has natural damping to return it to an equilibrium position. The response is always an exponential function (e^-j*omega*t) or (e^-omega*t) depending on if you are underdamped or overdamped.
The point is that an exponential decay envelop tells you how the response will change over time. And so when when I look at the velocity, I am able to fit an exponential decay envelope very nicely over the peaks.
This works very well describing the velocity behavior from mid last year to mid this year.
The last couple of months up to Now is where things get very interesting.
So for a physical system, the vibrations damp out to zero as time increases. And for very big disturbances, I would expect the market to behave like a physical system (it has mass, inertia, capacitance, etc. Tastylunch and I have had long conversations about this http://caps.fool.com/Blogs/ViewPost.aspx?bpid=127072, comments #39-43). The are places where these analogies do not work, but you can get a surprising amount of insight into monetary policy effects and assets price responses if you look at them as signal functions.
So the current large wave up (Primary 2) is a mechanism by the market to dampen out the oscillations caused by Primary 1 (the wave down last year). And from the decay envelopes above, you can see it was doing exactly that. But now the oscillations have begun to increase again. They are no longer being held in by the decay envelope.
And this goes directly to the observations that I made in my last post Recipe for Disaster. The market internals (and breadth is by far the most important internal measure) are becoming more violent up and down even as the price action narrows and starts going sideways / slightly up as it has the past couple of months.
This lets you know that there is a lot of turmoil beneath the surface and another large "step function" in price change is about to occur. Will it be a crash up or a crash down? I obviously have my opinion on the matter. For those who are interested in my opinion, please read this post: My Positions and Projections
But the real point of this post and the last post is to show that things are not as calm as they might appear on the surface.


